近日,我院罗伯特教授团队与南非金山大学研究团队合作,仅利用光的轨道角动量,在纠缠光子内部发现了一个丰富的、之前未知的拓扑结构。团队利用由纯轨道角动量纠缠构成的斯格明子,建立了与高能物理中非阿贝尔单极子纹理之间的直接对应,并提出了一种可扩展的高维量子态“拓扑谱”。相关成果以标题“Revealing the topological nature of entangled orbital angular momentum states of light”发表于《Nature Communications》,罗伯特教授为第一作者,我校为第一单位。
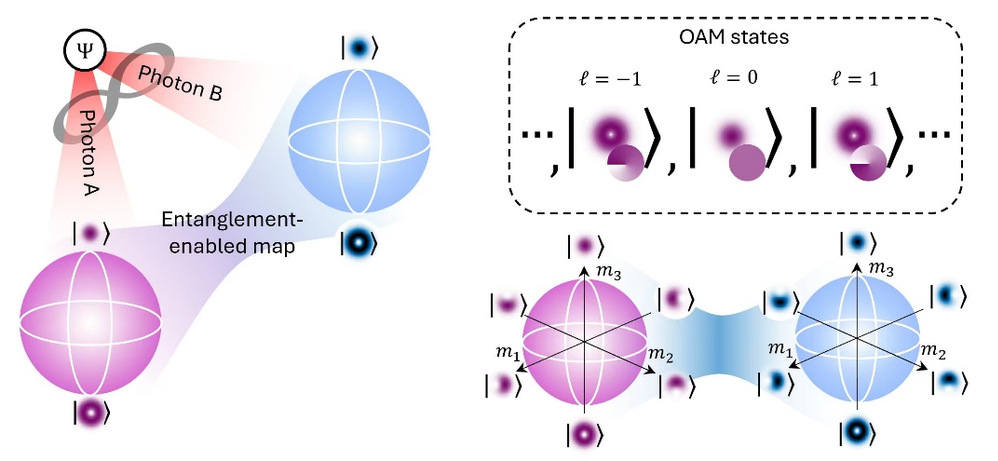
图1. 源自轨道角动量纠缠的斯格明子。纠缠在两个轨道角动量球面之间定义了一种映射,测得的缠绕数仅用轨道角动量即确认了斯格明子与反斯格明子结构。
该工作表明,拓扑可以被视为纠缠的内禀性质而非模拟效应,从而为更稳健的量子通信、量子传感和量子计算开辟了新途径。由于仅依赖轨道角动量,无需预先偏振化,该方法与现有结构光平台具有广泛兼容性,并可扩展到更高维。
我院罗伯特教授表示:“令人兴奋的是,我们观测到的拓扑并非人为设计——它早已存在于纠缠态之中。通过直接揭示和测量它,我们把台式光学实验与单极子和希格斯场的数学理论联系起来,同时为高维量子技术创造了新的资源。” 金山大学的安德鲁·福布斯教授补充道:“仅用 轨道角动量,我们突破了传统的偏振范式。由此产生的拓扑谱随着维数的增加呈现出爆炸式增长,为量子信息提供了一种规模庞大且具备抗噪性的高维量子态字集。”

图2. 双光子—单极子对应。该光学映射对应于’t Hooft–Polyakov 单极子的渐近希格斯场纹理,从而将实验与规范场论联系起来。
关键发现主要包括:(1) 首个仅基于轨道角动量的斯格明子:团队在由纠缠定义的两个 OAM“球面”之间,创建并测量了斯格明子/反斯格明子映射。(2) 双光子—单极子关联:同一映射对应于’t Hooft–Polyakov单极子的希格斯场渐近纹理,将光学测量与规范理论的基石相连接。(3) 高维“拓扑谱”:在维度为3、5、7时,由 SU(d) 组织的不同嵌入子流形各自携带绕数,随着 d 增大产生成千上万的候选不变量。(4) 既稳健又敏感:在现实噪声下,非平凡特征依然存在;同时可以在先前平凡的子空间中有意诱导出新特征——既有利于抗扰,也便于信道诊断。
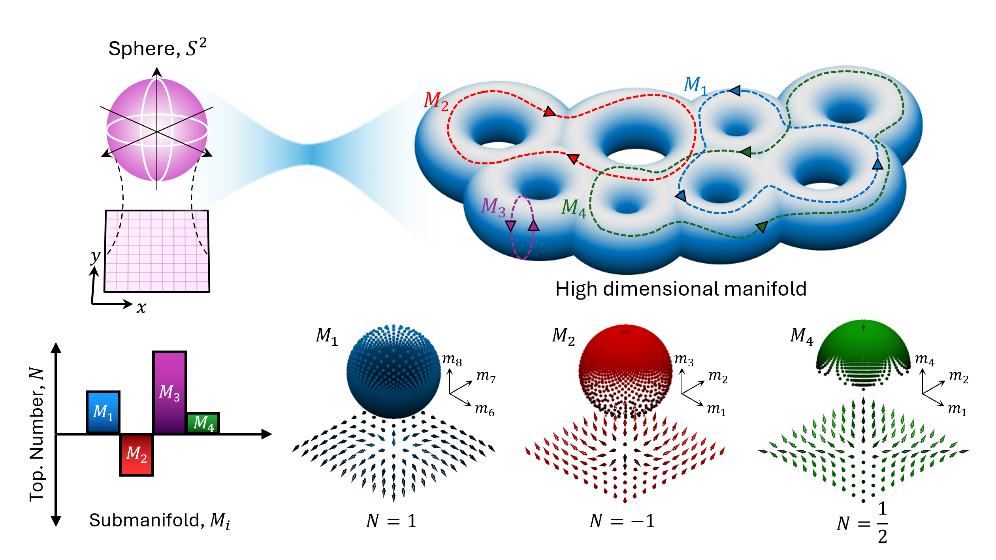
图3. 更高维度中的拓扑谱。由三维的测量谱以及在五维和七维示例显示,不同的拓扑特征随维度提升而快速增长。
本研究具有重要应用价值。利用高维纠缠是实现安全量子通信与先进量子传感的关键前沿,而拓扑化描述带来了两大优势,即稳定性(拓扑特征对小扰动具有鲁棒性)与可扩展性(可用的“字母表”随维度迅速增长)。本研究提供了一个直接、以实验为基础的框架,用于测量、认证并利用这种拓扑。
本项目由我校与南非金山大学结构光团队合作完成。团队成员包括罗伯特、Pedro Ornelas、Neelan Gounden、卢伯强、Isaac Nape和Andrew Forbes。
论文链接:https://www.nature.com/articles/s41467-025-66066-3.pdf



